《暗黑3》绝对堪称史诗级别的角色扮演类游戏,该作的人物角色成长系统以及武器装备系统都非常丰富,游戏的战斗过程中使用大量的绚丽技能,很多玩家对于暗黑3游戏中武器白字附魔的规律不是很了解,下面给大家用数据来分析。
前言:娜枪洗到2800有多难?一把千载难逢的灾虐/星铁/沃尔究竟洗到什么时候才应该收手?武器伤害这一词缀又是如何随机生成的?本贴带你探究其中规律
测试对象:

我们从10ed娜枪开始讲起。弩枪上的的伤害词缀随机范围是(858-1049)-(1028-1304),那么在生成随机词缀的时候,是不是在858-1049的范围内随机产生一个伤害下限,然后独立地在1028-1304的范围内随机产生一个伤害上限呢?
实践是检验真理的唯一标准,楼主将30次附魔产生的共计57个伤害词缀的记录了下来,如下图所示:
这里x轴表示最小伤害,y轴表示最大伤害,每个点就是一个(最小伤害-最大伤害)的词缀:

从这张分布图中可以看出,最大伤害和最小伤害并不是独立生成的,那么生成规律又是什么呢?
在图中加入两条斜率为1的直线,规律就显现出来了:

所有点近似均匀的分布在这个平行四边形区域内。斜率为1的直线代表着(最大伤害-最小伤害)这一差值为常数的点。从这一点,我们可以推断,武器伤害词缀的生成规律是:
第一步,随机生成一个最小伤害词缀,范围就是数据库中的最小伤害的随机范围;第二步,随机生成一个最大伤害和最小伤害的差值,其范围是(最大伤害下限-最小伤害下限)-(最大伤害上限-最小伤害上限)(即图中两条虚线所代表的的数值);最后,通过最小伤害+差值计算出最大伤害。
下面我们再用第二把武器检验一下刚才的结论。
楼主又记录了这把星铁附魔10次的结果,共计产生16个武器伤害词缀,其分布如下:

可以看到,结果完全符合我们理论的预期,可以推测这一规律适用于所有武器。
各位也可以通过自己手中的武器验证这一规律:最大伤害与最小伤害的差值不会超出(最大伤害上限-最小伤害上限)这一数值。
例如,一个伤害接近满的弩枪,其伤害有可能是1049-1290,但绝不可能出现1035-1304这种数值。
了解了这一规律之后,我们就可以计算洗出xxxx以上白字的概率了。
还是娜枪为例,现在的伤害词缀是1045-1272,我们在图中将这个点标下。只要最小伤害+最大伤害=1045+1272,武器的白字就和现在一样,所以,在图中,这一武器白字所对应的点可以用一条斜率为-1的直线来表示,而这条直线以上的部分(阴影部分),就是白字比现在高的部分。
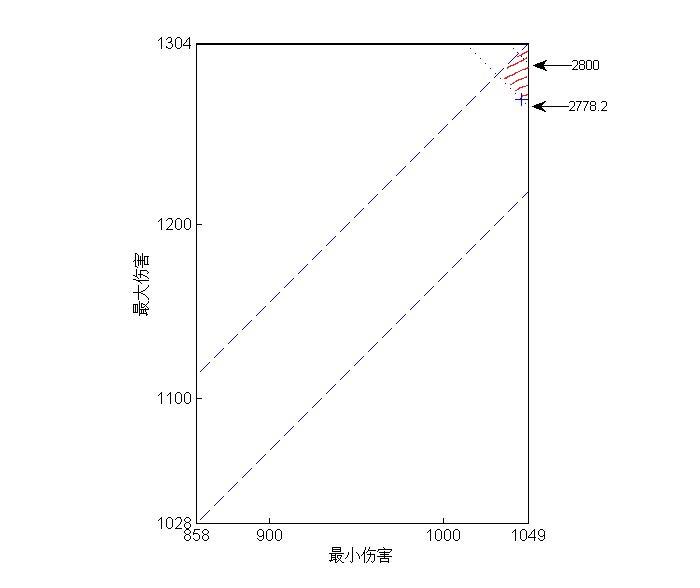
由于随机的伤害词缀在平行四边形区域内是均匀分布,随机出更高白字的概率,就等于阴影部分面积/整个平行四边形面积
如果用公式表示的话,就是:
(d1=最小伤害下限, d2=最小伤害上限,u1=最大伤害下限, u2=最大伤害上限,d=当前最小伤害,u=当前最大伤害)
平行四边形的面积=(d2-d1)*[(u2-d2)-(u1-d1)]
阴影面积=1/4*[(d2+u2)-(d+u)]^2 (注:仅适用于与白字较高的情况,即d+u>2*d2+u1-d1)
所以随机到更高白字的概率=1/4*[(d2+u2)-(d+u)]^2/{(d2-d1)*[(u2-d2)-(u1-d1)]}
代入这一公式,得出楼主这个娜枪洗出更高白字的概率是2.0%.(事实上在测试过程中已经出现了更高的白字)
而对于10ed娜枪,想让白字达到2800,通过以上公式计算得到的概率则是0.19%。
也就是说,想要洗出2800+的娜枪,忽略其他词缀出现的概率,每次附魔随机两个伤害词缀,你平均需要附魔1/(2*0.19%)=263次才能见到一次2800+的白字。
更新:
下表列出了根据上面公式的计算结果,各种武器洗出xxxx伤害的概率。
使用方法:以楼主的星铁为例,现在的伤害是1194-1455,极限值是1199-1490,差距就是(1199+1490)-(1194+1455)=40,在下表中,差距40对应的概率是1.89%,也就是说一个随机伤害有1.89%的概率比楼主现在的伤害高。(一次附魔产生2个随机词缀,假设都是伤害词缀,那么每次附魔洗出更高白字的概率大约就是2*1.89%=3.78%)
| 最大伤害+最小伤害与极限值的差距 | 1.2-1.4速单手,弓,弩 (极值1199-1490) | 匕首,弩枪 (极值1049-1304) | 双手武器 (极值1439-1788) |
| 5 | 0.03% | 0.04% | 0.02% |
| 10 | 0.12% | 0.15% | 0.08% |
| 20 | 0.47% | 0.62% | 0.33% |
| 30 | 1.06% | 1.39% | 0.74% |
| 40 | 1.89% | 2.46% | 1.32% |
| 50 | 2.96% | 3.85% | 2.06% |
| 60 | 4.26% | 5.54% | 2.96% |
| 70 | 5.79% | 7.55% | 4.03% |
| 80 | 7.57% | 9.86% | 5.26% |

